关键词： 全国招教

《终边相同的角》

内容：

探究

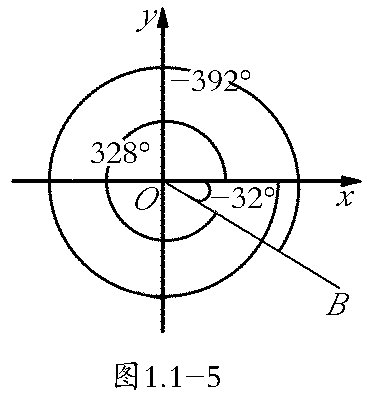
将角按照上述方法放在直角坐标系中后，给定一个角，就有唯一的一条终边与之对应。反之，对于直角坐标系内任意一条射线[OB]（如图1.1-5），以它为终边的角是否唯一？如果不唯一，那么终边相同的角有什么关系？

不难发现，在图1.1-5中，如果-32°的终边是[OB]，那么328°，-392°…角的终边都是OB，并且与-32°角终边相同的这些角都可以表示成-32°的角与[k]个（[k∈Z]）周角的和，如：

[328°=-32°+360°]（这里[k=]    ）

[-392°=-32°-360°]（这里[k=]    ）设[S=β｜β=-32°+k·360°，k∈Z]，则328°，-392°角都是[S]的元素，-32°角也是[S]的元素（此时[k=]         ）。因此，所有与-32°角终边相同的角，连同-32°角在内，都是集合[S]的元素；反过来，集合[S]的任一元素显然与-32°角终边相同。

一般地，我们有：

所有与角α终边相同的角，连同角α在内，可构成一个集合

[S=β｜β=α+k·360°，k∈Z]，

即任一与角α终边相同的角，都可以表示成角α与整数个周角的和。

例1 在0°~360°范围内，找出与-950°12′角终边相同的角，并判定它是第几象限角。

基本要求：

（1）要有板书；

（2）条理清晰，重点突出；

（3）教学过程注意启发引导。

答辩题目：

1.简述本节内容在教材中的作用与地位。

2.在本节课的教学过程中，你是如何突破难点的？

试讲答案：

各位考官：大家好，我是高中数学组的XX号考生，我试讲的题目是《终边相同的角》，下面开始我的试讲。

一、导入新课

师：在直角坐标系中，以原点为定点，x轴正半轴为始边，画出210°，-45°以及-150°这三个角，它们的终边有什么特点？

师：学生1说210°与-150°这两个角的终边相同。

师：在练习本上画一条射线OA，把笔端与射线端点重合，将笔先转动到平面的一个位置OB，然后再按照顺时针方向或逆时针方向旋转笔，观察笔重复转到OB的位置时所形成角的特征。

师：学生2说这两个角的终边都在OB上。

师：给定一个角，就有唯一一条终边与之对应，反之，对于直角坐标系中的任意一条射线OB，以它为终边的角是否唯一？

师：学生3说不唯一，因为这样的角有很多个。

师：对，这些都是终边相同的角。今天我们就来学习终边相同的角。

>>全国教师招聘官方客服微信<<

注意：备注网站才能通过哟！！！

公告解读 _历年考情_备考指导_海量资料_精品课程

如有任何报考疑问，添加客服老师微信咨询

二、生成新知

师：在直角坐标系中标出210°，-150°，328°，-32°，-392°表示的角，观察它们的终边，你有什么发现？

师：210°和-150°的终边相同，328°，-32°，-392°的终边相同。

师：-32°是射线绕坐标原点旋转到-32°角终边的位置，-392°，328°分别是-32°继续按顺时针或逆时针方向再旋转一周所形成的角。显然，这三个角的终边相同，它们叫做终边相同的角。

师：这两组终边相同的角之间有什么数量关系？终边相同的角又有什么关系？

师：学生4说210°-（-150°）=360°，328°-（-32°）=360°，-32°-（-392°）=360°。学生5说由这两组角可以看出终边相同的角之间相差360°的整数倍。

师：那么对于这些角，我们如何用学过的数学语言将它们表示出来？

师：学生6说可以用描述法、用集合表示。

师：用集合的方式更方便也更加容易理解。设S={β|β=-32°+k·360°，k∈Z}，则328°，-392°角都是S的元素，-32°角也是S的元素（此时k=0）。因此，所有与-32°角的终边相同的角，连同-32°在内，都是集合S的元素；反过来，集合S的任何一个元素显然与-32°角终边相同。所有与α终边相同的角，连同角α在内，可以构成一个集合S={β|β=k·360°+α，k∈Z}。即任一与角α终边相同的角，都可以表示成α与整数个周角的和。

三、应用新知

师：在0°～360°范围内，找出与-950°12′角终边相同的角，并判定它是第几象限角。

师：学生7说是129°48′，在第二象限。

师：写出终边在y轴上的角的集合及终边在x轴上的角的集合。

师：同学们都写得很好。

四、小结作业

师：通过这节课的学习，你有什么收获？你对今天的学习还有什么疑问吗？预习下节课。

师：好，下课，同学们再见！

五、板书设计

终边相同的角

所有与α终边相同的角，连同角α在内，可以构成一个集合S={β|β=k·360°+α，k∈Z}。

表示方法：集合

特点：k∈Z；α是任意角；终边相同的角不一定相等，有无数多个，它们之间相差360°的整数倍。

我的试讲到此结束，谢谢各位考官的聆听！

答辩答案：

1.本课是数学必修四三角函数中第一节的内容。三角函数是基本初等函数，它是描述周期现象的重要数学模型。角的概念的推广正是这一思想的体现之一，是初中相关知识的自然延续。为进一步研究角的和、差、倍、半关系提供了条件，也为今后学习解析几何、复数等相关知识提供了有利的工具，所以学生正确的理解和掌握角的概念的推广尤为重要。

2.学生的活动过程决定着课堂教学的成败，教学中应反复挖掘“探究”栏目及“探究”示图的过程功能，在这个过程上要不惜多花些时间，让学生进行操作与思考，自然地、更好地归纳出终边相同的角的一般形式，也就自然地理解了集合S={β|β=α+k·360°，k∈Z}的含义。如能借助信息技术，则可以动态表现角的终边旋转的过程，更有利于学生观察角的变化与终边位置的关系，让学生在动态的过程中体会既要知道旋转量，又要知道旋转方向，才能准确刻画角的形成过程，更好地了解任意角的深刻涵义。

2024年教师招聘官方微信客服

• 公告资讯
• 学习答疑
• 1对1指导
• 笔试资料
• 面试技巧
• 公开讲座

手机微信扫描左侧二维码，添加客服老师微信领取